Solar Micro Car Kit DIY STEM Kit
$7.99$4.95
Posted on: Mar 14, 2011
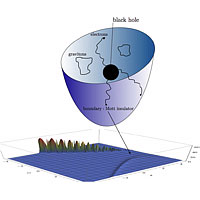
Mottness from a Black Hole
Black holes are some of the heaviest objects in the universe. Electrons are some of the lightest. Now physicists Robert G. Leigh and Philip Phillips along with postdoctoral fellow Mohammad Edalati and graduate student Ka Wai Lo of the University of Illinois have shown how charged black holes can be used to model the behavior of interacting electrons in unconventional superconductors.
“The context of this problem is high-temperature superconductivity,” said Phillips. “One of the great unsolved problems in physics is the origin of superconductivity (a conducting state with zero resistance) in the copper oxide ceramics discovered in 1986.” The group's research results were published online in Physical Review Letters on March 1 and in Physical Review D on February 25.
Unlike the old superconductors, which were all metals, the new superconductors start off their lives as insulators. In the insulating state of the copper-oxide materials, there are plenty of places for the electrons to hop but nonetheless—no current flows. Such a state of matter, known as a Mott insulator after the pioneering work of Sir Neville Mott, arises from the strong repulsions between the electrons. Although this much is agreed upon, much of the physics of Mott insulators remains unsolved, because there is no exact solution to the Mott problem that is directly applicable to the copper-oxide materials.
Enter string theory—an evolving theoretical effort that seeks to describe the known fundamental forces of nature, including gravity, and their interactions with matter in a single, mathematically complete system.
In string theory, some strongly interacting quantum mechanical systems can be studied by replacing them with classical gravity in a space-time in one higher dimension, a relationship that was first conjectured by string theorist Juan Maldacena some fourteen years ago. The conjecture was made possible by thinking about D-branes, important objects in string theory, in two different but equivalent ways. Physical features of the quantum systems, such as temperature, charge density, etc., become properties of black holes in the classical gravity theory.
Since most condensed matter phenomena involve electron physics, Leigh, along with graduate student Juan Jottar, set out to investigate the sorts of interactions that electrons might have in classical gravity theories that arise in string theory. Since the Mott problem is an example of strongly interacting particles, Edalati, Leigh, and Philips then asked the question: “Is it possible to devise a theory of gravity that mimics a Mott insulator?” Indeed it is.
The researchers built on Maldacena’s mapping and devised a model for electrons moving in a curved space-time in the presence of a charged black hole that captures two of the striking features of the normal state of high-temperature superconductors: 1) the presence of a barrier for electron motion in the Mott state, and 2) the strange metal regime in which the electrical resistivity scales as a linear function of temperature, as opposed to the quadratic dependence exhibited by standard metals.
The treatment advanced in the paper published in Physical Review Letters represents the first time a resolution of the Mott problem has been observed in a two-dimensional system, the relevant dimension for the high-temperature superconductors. The next big question that must be addressed is how does superconductivity might emerge from the gravity theory of a Mott insulator.
 'There comes a time when the mind takes a higher plane of knowledge but can never prove how it got there. All great discoveries have involved such a leap. The important thing is not to stop questioning.'
'There comes a time when the mind takes a higher plane of knowledge but can never prove how it got there. All great discoveries have involved such a leap. The important thing is not to stop questioning.'