Solar Micro Car Kit DIY STEM Kit
$7.99$4.95
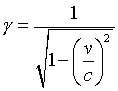
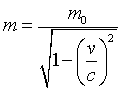

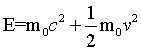
 'A hundred times every day I remind myself that my inner and outer life are based on the labors of other men, living and dead, and that I must exert myself in order to give in the same measure as I have received and am still receiving…'
'A hundred times every day I remind myself that my inner and outer life are based on the labors of other men, living and dead, and that I must exert myself in order to give in the same measure as I have received and am still receiving…'