Doodling Shake Bot DIY STEM Kit | xUmp.com Creative Robotics + Drawing Kit
$9.99$5.95
 Eigenvalues are multipliers. They are numbers that represent how much stretching has taken place or, in other words, how much something has been scaled up by. In the sentence 'I am 3.2 times taller than when I was born' the number 3.2 is acting as an eigenvalue.
To make sense of an eigenvalue it must have an associated 'operation' (the transformation that has occurred) and an associated 'direction' (the eigenvector). It doesn't mean anything by itself to say that 3.2 is an eigenvalue. You need to know the operation 'enlarged' and the direction "up" to say that I am now 3.2 times bigger in the up-direction !
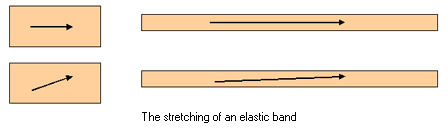
If you rotate a coin by 360 degrees you preserve all directions and so each direction is an eigenvector. Because no stretching has occurred, all of these eigenvectors have eigenvalue 1. Rotating the coin by 60 degrees destroys all directions and this transformation has no eigenvectors or eigenvalues at all. Careful spreading of butter on bread, by moving the knife in one direction only, is a transformation with an eigenvector in the direction of spreading. The associated eigenvalue depends on how far the butter is spread. The elastic band in the picture has an eigenvector in the left-right direction because that arrow still points in that direction after the transformation. The band has been stretched by approximately the same amount that I have grown since I was born - so the eigenvector has eigenvalue 3.2 !
The idea of eigenvalues and eigenvectors can be extended to any operator H. (H might be 'rotate by 360 degrees' or 'stretch in direction of y-axis' or operators in Quantum theory or elsewhere). We write H(x) to mean 'the action of H on x'. (So x might be a particular vector that we are rotating or stretching or it might be a quantum state or some other object). If we can find an object x and a number k so that the following equation is true:
H(x) = k * x
Then we know that x has been preserved by H apart from a scalar multiplier k. It is k times bigger than what it was before H acted upon it. Therefore we call x an eigenvector of H with eigenvalue k.
Eigenvalues are multipliers. They are numbers that represent how much stretching has taken place or, in other words, how much something has been scaled up by. In the sentence 'I am 3.2 times taller than when I was born' the number 3.2 is acting as an eigenvalue.
To make sense of an eigenvalue it must have an associated 'operation' (the transformation that has occurred) and an associated 'direction' (the eigenvector). It doesn't mean anything by itself to say that 3.2 is an eigenvalue. You need to know the operation 'enlarged' and the direction "up" to say that I am now 3.2 times bigger in the up-direction !
If you rotate a coin by 360 degrees you preserve all directions and so each direction is an eigenvector. Because no stretching has occurred, all of these eigenvectors have eigenvalue 1. Rotating the coin by 60 degrees destroys all directions and this transformation has no eigenvectors or eigenvalues at all. Careful spreading of butter on bread, by moving the knife in one direction only, is a transformation with an eigenvector in the direction of spreading. The associated eigenvalue depends on how far the butter is spread. The elastic band in the picture has an eigenvector in the left-right direction because that arrow still points in that direction after the transformation. The band has been stretched by approximately the same amount that I have grown since I was born - so the eigenvector has eigenvalue 3.2 !
The idea of eigenvalues and eigenvectors can be extended to any operator H. (H might be 'rotate by 360 degrees' or 'stretch in direction of y-axis' or operators in Quantum theory or elsewhere). We write H(x) to mean 'the action of H on x'. (So x might be a particular vector that we are rotating or stretching or it might be a quantum state or some other object). If we can find an object x and a number k so that the following equation is true:
H(x) = k * x
Then we know that x has been preserved by H apart from a scalar multiplier k. It is k times bigger than what it was before H acted upon it. Therefore we call x an eigenvector of H with eigenvalue k.
 'Physicists like to think that all you have to do is say, these are the conditions, now what happens next?'
'Physicists like to think that all you have to do is say, these are the conditions, now what happens next?'