Battery-Powered Balancing Robot DIY STEM Kit
$8.99$4.95
 Today, sea navigators measure their ship's speed using modern GPS (Global Positioning System) driven devices like one shown in the image to the right.
Today, sea navigators measure their ship's speed using modern GPS (Global Positioning System) driven devices like one shown in the image to the right. A good question one could ask now is: What did the sea navigators use for speed measurement before the GPS?
A good question one could ask now is: What did the sea navigators use for speed measurement before the GPS?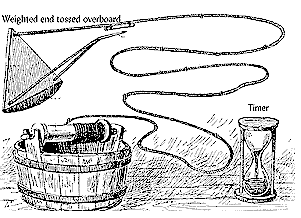 Rope had knots tied at equal distances along the reel. Sailors would throw the wood panel into the sea, behind the ship, and the rope would start unwinding from the reel. The faster the ship was moving forward the faster the rope would unwind. By counting the number of knots that went overboard in a given time interval, measured by the sand glass, they could tell the ship's speed.
In fact that is the origin of the nautical speed unit: the knot.
Rope had knots tied at equal distances along the reel. Sailors would throw the wood panel into the sea, behind the ship, and the rope would start unwinding from the reel. The faster the ship was moving forward the faster the rope would unwind. By counting the number of knots that went overboard in a given time interval, measured by the sand glass, they could tell the ship's speed.
In fact that is the origin of the nautical speed unit: the knot. |
 So, how fast is a 'knot'?
So, how fast is a 'knot'?Well, first we should know that for distance sailors used (and still use) the so called 'nautical mile'. If you slice Earth into two equal halves right through its center along equator for example, then divide the perimeter (the circumference) into 360 degrees, then each degree into 60 arc minutes, the length you get is approximately 1 nautical mile. So, to recap, one nautical mile is the arc distance of about 1 minute of a degree (or 1/60th of a degree) of Earth. We say approximate because if you choose to slice Earth along the line that goes through the North and South poles you would get a slightly different result due to the fact that Earth is not a perfect sphere - it is slightly flattened at the poles. Difference between the polar and equatorial diameter being about 23.4 nautical miles out of 6880 nautical miles. Exact value for the nautical mile is taken to be the average of the two (polar and equatorial) and is: 1 nautical mile = 1.15 miles = 1852 meters = 6067 feet Naturally, sailors wanted to have their ship's speed in units of nautical miles per hour (just like American car drivers like their car speed in miles per hour - my apologies to the rest of the world. However, don't fuss too much since the meter was also defined quite arbitrary around 17th century as one part in 10 million of the distance from the North Pole to the Equator along the meridian of Paris.) To avoid ropes that were miles and miles in length, they usually had ropes that had knots every 50 feet and a sand glass that measured half a minute. If you work out the math you will convince yourself that the number of knots that went overboard in half a minute is exactly the number of nautical miles per hour the ship was cruising at. For example, if 10 knots went overboard in half a minute, then the ship was moving forward at the speed of 10 knots or 10 nautical miles per hour (which would be about 11.5 standard miles per hour.) Records from 1917 (Bowditch) indicate that the official U.S. Navy sand glass measured 28 seconds, and that knots were spaced out exactly 48 feet (or 8 fathoms - a popular length unit of that time). With this setup, ship's speed could be measured with an error of about 1.5%. This is speed relative to the water and assuming that the wood panel does not get pulled significantly from the place where it was initially dropped and that the rope does not stretch - all of which actually does happen and should be accounted as sources of error. Not to mention the problem of sea water currents adding or subtracting from the actual ship's speed relative to land. There you go, from knots to GPS, human ingenuity surprises and inspires once again! If you would like to learn more, here are some resources: On GPS: National Air and Space Museum On the History of Navigation: Boatsafe.com On the Chip Log: Heaving the Log and Dead Reckoning and the Chip Log Images are copyright of owners as indicated below each image. Posted with permission. Visit Michael Halbert's website (author of the Old Ship image above) for more interesting artwork: http://www.inkart.com/ Answered by: Anton Skorucak, M.S. Physics, Creator of PhysLink.com, California, USA  'Arrows of hate have been shot at me too, but they have never hit me, because somehow they belonged to another world with which I have no connection whatsoever.'
'Arrows of hate have been shot at me too, but they have never hit me, because somehow they belonged to another world with which I have no connection whatsoever.'Albert Einstein (1879-1955) Top 100 Lists:Popular Products:
Science Articles:Shop Our Online Science Store© Copyright 1995-2024 PhysLink.com
|