Fan Micro Car DIY STEM Kit
$9.99$5.55
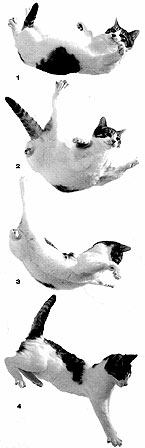 Cats have the seemingly unique ability to orient themselves in a fall allowing them
to avoid many injuries. This ability is attributed to two significant feline
characteristics: A 'righting reflex' and a unique skeletal structure.
Cats have the seemingly unique ability to orient themselves in a fall allowing them
to avoid many injuries. This ability is attributed to two significant feline
characteristics: A 'righting reflex' and a unique skeletal structure.
 'If one wishes to obtain a definite answer from Nature one must attack the question from a more general and less selfish point of view.'
'If one wishes to obtain a definite answer from Nature one must attack the question from a more general and less selfish point of view.'