Wire Maze Electricity DIY STEM Kit
$8.99$4.95
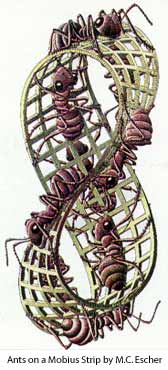 Very roughly a surface is orientable if it has two sides so that, for example, is
it possible to paint it with two different colours. A sheet of paper or the
surface of a sphere are examples of orientable surfaces. A Mobius strip is a
non-orientable surface: you can build one with a strip of paper (twist the strip
and glue end together to form a ring) and verify that it has only one side: it is
not possible to paint it with two colours.
Very roughly a surface is orientable if it has two sides so that, for example, is
it possible to paint it with two different colours. A sheet of paper or the
surface of a sphere are examples of orientable surfaces. A Mobius strip is a
non-orientable surface: you can build one with a strip of paper (twist the strip
and glue end together to form a ring) and verify that it has only one side: it is
not possible to paint it with two colours.
