Fan Micro Car DIY STEM Kit
$9.99$5.95
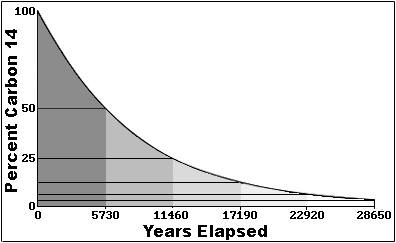
 So in the real world, looking at a sample like say a bone dug up by an
archaeologist, how do we know how much carbon 14 we started with? That's actually
kind of cool. It's a semi-long story, so bear with me. In the atmosphere, cosmic
rays smash into normal carbon 12 atoms (in atmospheric carbon dioxide), and create
carbon 14 isotopes. This process is constantly occurring, and has been for a very
long time, so there is a fairly constant ratio of carbon 14 atoms to carbon 12
atoms in the atmosphere. Now living plants 'breathe' CO2 indiscriminately (they
don't care about isotopes one way or the other), and so (while they are living)
they have the same ratio of carbon 14 in them as the atmosphere. Animals,
including humans, consume plants a lot (and animals that consume plants), and thus
they also tend to have the same ratio of carbon 14 to carbon 12 atoms. This
equilibrium persists in living organisms as long as they continue living, but when
they die, they no longer 'breathe' or eat new 14 carbon isotopes
Now it's fairly simple to determine how many total carbon atoms should be in a
sample given its weight and chemical makeup. And given the fact that the ratio of
carbon 14 to carbon 12 in living organisms is approximately 1 : 1.35x10-12, we can
figure out how many carbon 14 atoms were in the sample when it ceased to replenish
it's supply.
So in the real world, looking at a sample like say a bone dug up by an
archaeologist, how do we know how much carbon 14 we started with? That's actually
kind of cool. It's a semi-long story, so bear with me. In the atmosphere, cosmic
rays smash into normal carbon 12 atoms (in atmospheric carbon dioxide), and create
carbon 14 isotopes. This process is constantly occurring, and has been for a very
long time, so there is a fairly constant ratio of carbon 14 atoms to carbon 12
atoms in the atmosphere. Now living plants 'breathe' CO2 indiscriminately (they
don't care about isotopes one way or the other), and so (while they are living)
they have the same ratio of carbon 14 in them as the atmosphere. Animals,
including humans, consume plants a lot (and animals that consume plants), and thus
they also tend to have the same ratio of carbon 14 to carbon 12 atoms. This
equilibrium persists in living organisms as long as they continue living, but when
they die, they no longer 'breathe' or eat new 14 carbon isotopes
Now it's fairly simple to determine how many total carbon atoms should be in a
sample given its weight and chemical makeup. And given the fact that the ratio of
carbon 14 to carbon 12 in living organisms is approximately 1 : 1.35x10-12, we can
figure out how many carbon 14 atoms were in the sample when it ceased to replenish
it's supply.
 'As long as men are free to ask what they must; free to say what they think; free to think what they will; freedom can never be lost and science can never regress. '
'As long as men are free to ask what they must; free to say what they think; free to think what they will; freedom can never be lost and science can never regress. '