Doodling Shake Bot DIY STEM Kit
$9.99$5.95
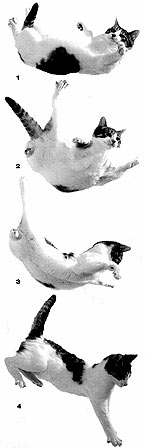 Cats have the seemingly unique ability to orient themselves in a fall allowing them
to avoid many injuries. This ability is attributed to two significant feline
characteristics: A 'righting reflex' and a unique skeletal structure.
Cats have the seemingly unique ability to orient themselves in a fall allowing them
to avoid many injuries. This ability is attributed to two significant feline
characteristics: A 'righting reflex' and a unique skeletal structure.
 'One cannot help but be in awe when he contemplates the mysteries of eternity, of life, of the marvelous structure of reality. It is enough if one tries merely to comprehend a little of this mystery every day.'
'One cannot help but be in awe when he contemplates the mysteries of eternity, of life, of the marvelous structure of reality. It is enough if one tries merely to comprehend a little of this mystery every day.'