Solar & Battery Fan DIY STEM Kit
$9.99$6.95
Posted on: Feb 9, 2012
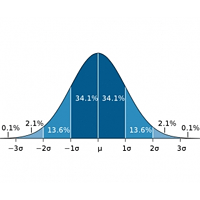
On this chart of a 'normal' distribution, showing the classic 'bell curve' shape, the mean (or average) is the vertical line at the center, and the vertical lines to either side represent intervals of one, two and three sigma. The percentage of data points that would lie within each segment of that distribution are shown.
Courtesy: MIT
It’s a question that arises with virtually every major new finding in science or medicine: What makes a result reliable enough to be taken seriously? The answer has to do with statistical significance — but also with judgments about what standards make sense in a given situation.
The unit of measurement usually given when talking about statistical significance is the standard deviation, expressed with the lowercase Greek letter sigma (s). The term refers to the amount of variability in a given set of data: whether the data points are all clustered together, or very spread out.
In many situations, the results of an experiment follow what is called a “normal distribution.” For example, if you flip a coin 100 times and count how many times it comes up heads, the average result will be 50. But if you do this test 100 times, most of the results will be close to 50, but not exactly. You’ll get almost as many cases with 49, or 51. You’ll get quite a few 45s or 55s, but almost no 20s or 80s. If you plot your 100 tests on a graph, you’ll get a well-known shape called a bell curve that’s highest in the middle and tapers off on either side. That is a normal distribution.
The deviation is how far a given data point is from the average. In the coin example, a result of 47 has a deviation of three from the average (or “mean”) value of 50. The standard deviation is just the square root of the average of all the squared deviations. One standard deviation, or one sigma, plotted above or below the average value on that normal distribution curve, would define a region that includes 68 percent of all the data points. Two sigmas above or below would include about 95 percent of the data, and three sigmas would include 99.7 percent.
So, when is a particular data point — or research result — considered significant? The standard deviation can provide a yardstick: If a data point is a few standard deviations away from the model being tested, this is strong evidence that the data point is not consistent with that model. However, how to use this yardstick depends on the situation. John Tsitsiklis, the Clarence J. Lebel Professor of Electrical Engineering at MIT, who teaches the course Fundamentals of Probability, says, “Statistics is an art, with a lot of room for creativity and mistakes.” Part of the art comes down to deciding what measures make sense for a given setting.
For example, if you’re taking a poll on how people plan to vote in an election, the accepted convention is that two standard deviations above or below the average, which gives a 95 percent confidence level, is reasonable. That two-sigma interval is what pollsters mean when they state the “margin of sampling error,” such as 3 percent, in their findings.
That means if you asked an entire population a survey question and got a certain answer, and then asked the same question to a random group of 1,000 people, there is a 95 percent chance that the second group’s results would fall within two-sigma from the first result. If a poll found that 55 percent of the entire population favors candidate A, then 95 percent of the time, a second poll’s result would be somewhere between 52 and 58 percent.
Of course, that also means that 5 percent of the time, the result would be outside the two-sigma range. That much uncertainty is fine for an opinion poll, but maybe not for the result of a crucial experiment challenging scientists’ understanding of an important phenomenon — such as last fall’s announcement of a possible detection of neutrinos moving faster than the speed of light in an experiment at the European Center for Nuclear Research, known as CERN.
Six sigmas can still be wrong
Technically, the results of that experiment had a very high level of confidence: six sigma. In most cases, a five-sigma result is considered the gold standard for significance, corresponding to about a one-in-a-million chance that the findings are just a result of random variations; six sigma translates to one chance in a half-billion that the result is a random fluke. (A popular business-management strategy called “Six Sigma” derives from this term, and is based on instituting rigorous quality-control procedures to reduce waste.)
But in that CERN experiment, which had the potential to overturn a century’s worth of accepted physics that has been confirmed in thousands of different kinds of tests, that’s still not nearly good enough. For one thing, it assumes that the researchers have done the analysis correctly and haven’t overlooked some systematic source of error. And because the result was so unexpected and so revolutionary, that’s exactly what most physicists think happened — some undetected source of error.
Interestingly, a different set of results from the same CERN particle accelerator were interpreted quite differently.
A possible detection of something called a Higgs boson — a theorized subatomic particle that would help to explain why particles weigh something rather than nothing — was also announced last year. That result had only a 2.3sigma confidence level, corresponding to about one chance in 50 that the result was a random error (98 percent confidence level). Yet because it fits what is expected based on current physics, most physicists think the result is likely to be correct, despite its much lower statistical confidence level.
Significant but spurious
But it gets more complicated in other areas. “Where this business gets really tricky is in social science and medical science,” Tsitsiklis says. For example, a widely cited 2005 paper in the journal Public Library of Science — titled “Why most published research findings are wrong” — gave a detailed analysis of a variety of factors that could lead to unjustified conclusions. However, these are not accounted for in the typical statistical measures used, including “statistical significance.”
The paper points out that by looking at large datasets in enough different ways, it is easy to find examples that pass the usual criteria for statistical significance, even though they are really just random variations. Remember the example about a poll, where one time out of 20 a result will just randomly fall outside those “significance” boundaries? Well, even with a five-sigma significance level, if a computer scours through millions of possibilities, then some totally random patterns will be discovered that meet those criteria. When that happens, “you don’t publish the ones that don’t pass” the significance test, Tsitsiklis says, but some random correlations will give the appearance of being real findings — “so you end up just publishing the flukes.”
One example of that: Many published papers in the last decade have claimed significant correlations between certain kinds of behaviors or thought processes and brain images captured by magnetic resonance imaging, or MRI. But sometimes these tests can find apparent correlations that are just the results of natural fluctuations, or “noise,” in the system. One researcher in 2009 duplicated one such experiment, on the recognition of facial expressions, only instead of human subjects he scanned a dead fish — and found “significant” results.
“If you look in enough places, you can get a ‘dead fish’ result,” Tsitsiklis says. Conversely, in many cases a result with low statistical significance can nevertheless “tell you something is worth investigating,” he says.
So bear in mind, just because something meets an accepted definition of “significance,” that doesn’t necessarily make it significant. It all depends on the context.
 'For the sake of persons of ... different types, scientific truth should be presented in different forms, and should be regarded as equally scientific, whether it appears in the robust form and the vivid coloring of a physical illustration, or in the tenuity and paleness of a symbolic expression.'
'For the sake of persons of ... different types, scientific truth should be presented in different forms, and should be regarded as equally scientific, whether it appears in the robust form and the vivid coloring of a physical illustration, or in the tenuity and paleness of a symbolic expression.'